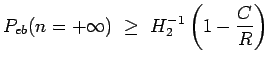Application to VDSL2
Turbo trellis coded modulations (TTCM) [4] have been proposed
for channel coding of VDSL2 using QAM modulations for a large range
of spectral efficiency values [8]. The TTCM is serially concatenated
with an outer code. The latter is a standard Reed-Solomon (RS) of length 255
and dimension 239 defined over the field  . As designed in [8],
a 128-QAM constellation is adequately partitioned and labelled, two bits in
a QAM symbol label are precoded with a rate
. As designed in [8],
a 128-QAM constellation is adequately partitioned and labelled, two bits in
a QAM symbol label are precoded with a rate  binary parallel turbo code
yielding a final spectral efficiency of 5 bits/sec/Hz. After taking into account
the RS coding rate, the information rate of RS+TTCM is
binary parallel turbo code
yielding a final spectral efficiency of 5 bits/sec/Hz. After taking into account
the RS coding rate, the information rate of RS+TTCM is
 bits
per real dimension. The TTCM block length is 1022 QAM symbols (Turbo interleaver of
size 2044 bits). Hence, the code is in a real space of dimension n=2044.
bits
per real dimension. The TTCM block length is 1022 QAM symbols (Turbo interleaver of
size 2044 bits). Hence, the code is in a real space of dimension n=2044.
Let us compare the performance of the RS+TTCM to the error rate of an optimal
code having the same parameters. In order to convert the word error probability  given by (2) into a bit error probability
given by (2) into a bit error probability  ,
we propose the following: Assume that a codeword on the n-dimensional
sphere is surrounded by
,
we propose the following: Assume that a codeword on the n-dimensional
sphere is surrounded by  neighbours and assume that decoding errors
yield only one of those neighbours. Each codeword is labelled by
neighbours and assume that decoding errors
yield only one of those neighbours. Each codeword is labelled by  bits.
The considered neighbours are labelled by
bits.
The considered neighbours are labelled by
 bits,
suppose that
bits,
suppose that
 . If random binary labelling is used to index
the
. If random binary labelling is used to index
the  neighbours, then we have
neighbours, then we have
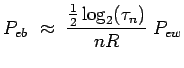 |
(3) |
Let  denote the greatest value attainded by the kissing number
of an n-dimensional sphere packing. It is known that [5]
denote the greatest value attainded by the kissing number
of an n-dimensional sphere packing. It is known that [5]
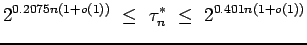 |
(4) |
The lower bound has been proved by Kabatiansky and Levenshtein [3]
and the upper bound by Wyner [2]. Finally by using the right inequality
in (4) we get
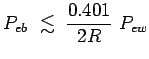 |
(5) |
Figure 5 illustrates the bit error rate of RS+TTCM versus optimal codes at finite length.
The coding gain gap is about 2.45 dB (3dB from capacity limit at  ).
The capacity limit is given by the rate-distortion bound
).
The capacity limit is given by the rate-distortion bound
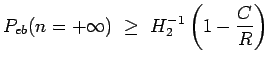 |
(6) |
Since  is the rate per real dimension, then
is the rate per real dimension, then
 .
Multilevel coded modulations with multistage decoding [6]
exhibit performance similar to those of RS+TTCM.
We believe that feasible coded modulations exist at less than 1dB
from optimal codes at such high information rates.
.
Multilevel coded modulations with multistage decoding [6]
exhibit performance similar to those of RS+TTCM.
We believe that feasible coded modulations exist at less than 1dB
from optimal codes at such high information rates.
Joseph Jean Boutros
2006-11-11